Wolfram Mathematica, Mathematica, пакеты, вопросы и ответы Опции

[Wild Bill]

Wolfram Mathematica


Год/Дата Выпуска: 2010
Версия: 8.0
Разработчик: Wolfram Research, Inc.
Сайт разработчика: http://www.wolfram.com/

Разрядность: 32bit+64bit
Совместимость с Vista: полная (есть на трекерах)
Совместимость с Windows 7: полная (есть на трекерах)
Совместимость с Linux: полная (есть на трекерах)
Язык интерфейса: Английский
Таблэтка: Отсутствует (годится от версии 4.0 и позже)
Системные требования:
Windows 7
Windows Vista
Windows XP
Windows Server 2008
Windows Server 2003
Windows Compute Cluster Server 2003
Windows 2000
Описание: Mathematica - программа, предназначеная для выполнения вычислений, для подготовки интерактивных документов и программирования.
Этот инструмент применяется в научных исследованиях, инженерном анализе и моделировании, для обучения в технических учебных заведениях.

Численные расчеты
* Существенно оптимизирована численная линейная алгебра плотных матриц.
* Новая оптимизированная линейная алгебра разреженных матриц.
* Поддержка оптимизированной линейной алгебры произвольной точности.
* Команда LinearSolveFunction для решения линейных систем уравнений для векторов матриц.
* Поддержка крупномасштабного линейного программирования методами внутренней точки.
* Новые методы и поддержка массивов переменных в командах FindRoot и FindMinimum.
* Команда FindFit для нелинейной аппроксимации кривыми.
* Команда глобальной оптимизации NMinimize.
* Поддержка решения n-мерных уравнений с частными производными в команде NDSolve.
* Поддержка решения алгебраических дифференциальных уравнений в команде NDSolve.
* Поддержка векторов и массивов в команде NDSolve.
* Чрезвычайно широкий набор автоматически вызываемых алгоритмов в команде NDSolve.
* Более высокая точность и контроль точности приближенных чисел.
* Высокая эффективность арифметики больших чисел, включая оптимизацию под конкретный процессор.
* Усиленные алгоритмы для операций в области теории чисел, включая GCD и FactorInteger.
* Прямая поддержка высокопроизводительных основных статистических функций.

Символьные расчеты
* Решение смешанных систем уравнений и неравенств командой Reduce.
* Полное решение полиномиальных систем в поле действительных и комплексных чисел.
* Решение широкого класса Диофантовых уравнений.
* ForAll и Exists кванторы и кванторное упрощение.
* Представление дискетных и непрерывных алгебраических и трансцендентных множеств решений.
* Команда FindInstance для нахождения примеров решений для различных областей определения переменных.
* Точная минимизация в полях целых и действительных чисел.
* Интегрированная поддержка допущений с помощью функций Assuming и Refine.
* RSolve для решения рекуррентных уравнений.
* Поддержка нелинейных и разностных уравнений и систем.
* Полное решение рациональных систем обыкновенных дифференциальных уравнений.
* Поддержка дифференциальных алгебраических уравнений.
* Команда CoefficientArrays для конвертирования систем уравнений в тензоры.

Программирование и системное ядро
* Интегрированная языковая поддержка разреженных массивов .
* Новые методы программирования списков с использованием Sow и Reap.
* EvaluationMonitor и StepMonitor для наблюдения за работой алгоритмов.
* Улучшенная система временных измерений, включающая функцию AbsoluteTiming.
* Существенное увеличение производительности для MathLink. * Новый модуль .NET/Link, позволяющий интегрировать пакет Mathematica с приложениями, использующими технологическую платформу Microsoft .NET Framework.
* Оптимизация под 64-битные операционные системы и архитектуры.
* Поддержка вычислений в 64-битных адресных пространствах.

Интерфейс
* Поддержка более 50 форматов экспорта и импорта.
* Высокоэффективный экспорт и импорт табличных данных.
* PNG, SVG и DICOM графики и форматы изображений.
* Импорт и экспорт форматов разреженных матриц.
* MPS формат линейного программирования.
* XHTML формат для экспорта рабочих документов.
* Улучшенный браузер подсказки.
* Улучшенная поддержка слайд-шоу презентаций.
* Улучшенная поддержка инструментов опубликования (AuthorTools).

И многое другое....

Сообщение отредактировал Wild Bill - 25.11.2010, 15:51

[Wild Bill]

Проводил испытания Mathematica 8 на скорость по её встренному тесту.
Windows 7 Ultimate x64 -- Index: 0.9;
CentOS 5.5 x64 -- Index: 1.1.
То есть на одной и той же машине вычисления под Linux на 20% быстрее. (IMG:style_emoticons/default/vse_ravno.gif)

[Wild Bill]

SusyMath - A Mathematica© package for quantum superfield calculations (пакет для работы с квантовыми суперполями).

SusyMath помогает проводить вычисления в квантовых суперполевых теориях. Он состоит из набора процедур для автоматического вычисления и упрощения суперграфов в суперсимметричных теориях трёх и четырёх пространственно-временных измерений.

SusyMath распространяется как свободное программное обеспечение с лицензией LGPL.

[Wild Bill]

Решение ОДУ с помощью рядов

Рассмотрим уравнение (y')^2 - y = x с начальным условием y(0) = 1.

Решение ОДУ с помощью рядов предполагает, что y[x] задано степенным рядом с неизвестными коэффициентами при x. Такой ряд строится с помощью встроенной функции SeriesData

Код

In[1]:= y[x_]:=SeriesData[x,0,Table[a[i],{i,0,7}], 0,8,1]
In[2]:= seriesDE=(Dt[y[x], x, Constants->Table[a[i],{i,0,7}]])^2-y[x]==x

Out[2]=

LogicalExpand[expression] раскрывает логические комбинации уравнений, неравенств и других функций

Код

In[3]:= coeffEqn=LogicalExpand[seriesDE]

Out[3]=

Полученную систему решаем при начальном условии a[0] == 1

Код

In[4]:= coeffSol=Solve[{coeffEqn,a[0]==1},Table[a[i],{i,0,7}]]

Out[4]=

Мы нашли два решения

Код

In[5]:= coeffSol[[2]]

Out[5]=

Подстановками получаем

Код

In[6]:=seriesSol2=y[x]/.Join[coeffSol[[2]],{a[0]->1}]

Out[6]=

Код

In[7]:=seriesSol1=y[x]/.Join[coeffSol[[1]],{a[0]->1}]

Out[7]=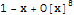
Заметим, что во входных ячейках выше мы используем команду Join для соединия списков.

Теперь проверяем :

Код

In[8]:= seriesDE/.coeffSol

Out[8]=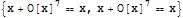

Функция Normal, применённая к выражению, преобразует это выражение в нормальную форму, то есть полим без члена О[x]^8

Код

In[9]:= sol2=Normal[seriesSol2]

Out[9]=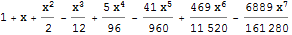

График решения на интервале [0, 2.5]

Код

In[10]:= Plot[sol2,{x,0,2.5}]

Out[10]=

[Wild Bill]

SARAH

SARAH -- это пакет для построения и анализа суперсимметричных моделей. Необходимо задать калибровку, содержание частиц и суперпотенциал для вычисления всей информации о собственных состояниях модели. Легко может быть добавлено нарушение калибровочной симмтерии и смешивание частиц.